Bellman Equation
벨만 방정식은 강화학습에서 필요한 가장 중요한 식 중 하나이다.
벨만 방적식은 현재 state와 이후 state들의 가치함수 ($ \nu_{\pi }(s), q_{\pi }(s, a) $) 사이의 관계를 식으로 나타낸 것이다.
수식은 다음과 같다. 수식이 조금 긴데 차근차근 알아보도록 하자.
State-value function에서의 Bellman Equation
$ \nu_{\pi }(s)\doteq E_{\pi }[G_{t}|S_{t}=s] $
$ = E_{\pi }[R_{t+1} + \gamma G_{t+1}|S_{t}=s] $
$ = \sum_{a}^{}\pi (a|s)\sum_{s'}^{}\sum_{r}^{}p(s', r|s, a) [r + \gamma E_{\pi }[G_{t+1}|S_{t+}=s']] $
$ = \sum_{a}^{}\pi (a|s)\sum_{s', r}^{}p(s', r|s, a) [r + \gamma\upsilon _{\pi }(s') ] $ , for all s $ \in S $
$ \sum_{a}^{}\pi (a|s) $ : current state s 에서 π에 의해 행할 수 있는 action들의 확률 합 (= 1)
$ sum_{s', r}^{}p(s', r|s, a) $ : current state s 에서 action a를 했을 때 next state s'에서 reward r을 받을 확률의 합 (= 1)
$ \gamma E_{\pi }[G_{t+1}|S_{t+}=s'] $ : next state s'에서의 기댓값 * (할인률)
$ upsilon _{\pi }(s') $ : next state s' 에서의 Bellman equation
마지막 식으로 정리할 수 있다.
current state의 value를 모든 이어지는 state들의 value와 현재의 보상값의 합으로 표현할 수 있다.
Action-value function에서의 Bellman Equation
특정 state-action pair의 value를 모든 가능한 next state-action value pair 와 reward의 합으로 표현된다.
state-value function이랑 다른점이 있다면 action별로 구분지은 것이 action-value function 에서의 bellman equation이라고 할 수 있다.
$$ q_{\pi }(s, a) = \sum_{s', r}p(s', r | s, a)[r + \gamma \sum _{a'}\pi (a'|s')q_{\pi }(s'|a')] $$
이 둘을 그림을 통해 비교를 해보자.

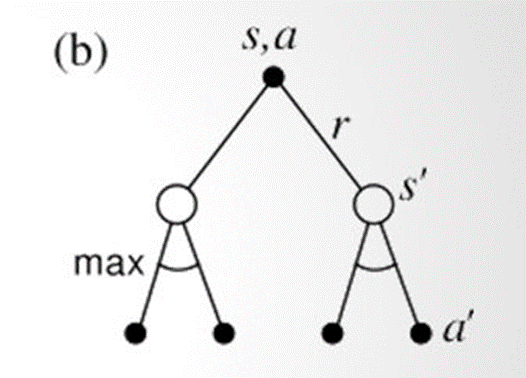
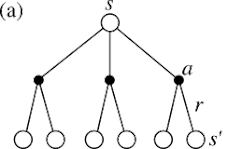
(a) 에서는 state-value function에서의 backup diagram을 보이고 있다.
state S 에서 π에 의해 3가지의 action을 할 수 있고, 그 중에서 action a를 통해 state s'로 가면서 reward r를 받을 수 있음을 보이고 있다.
$$ \upsilon _{\pi }(s) = \sum_{a}^{}\pi (a|s)\sum_{s', r}^{}p(s', r|s, a) [r + \gamma\upsilon _{\pi }(s') ] $$
(b) 에서는 action-value function에서의 backup diagram을 보이고 있다.
state S 에서 action a를 선택했을 때 next state s'로 갈 확률 p와, 그 s'에서 policy π에 의해 next action a'에 의한 bellman 값을 확인할 수 있다.
$$ q_{\pi }(s, a) = \sum_{s', r}p(s', r | s, a)[r + \gamma \sum _{a'}\pi (a'|s')q_{\pi }(s'|a')] $$
Bellman equation으로 최적 정책(Optimal Policy, $ \pi _{*} $)을 구해보자
Optimal Policy(최적 정책)은 다른 모든 정책보다 좋거나 같은 수준의 정책을 의미한다.
결국 Bellman equation이 존재하는 목적은 최적 정책을 찾기 위해 존재한다고 할 수 있고, 이것이 강화학습의 목표라고 할 수 있겠다.
Bellman Optimal State-Value Equation
쉽게 생각하면 Bellman 방정식을 Bellman 최적 방정식으로 바꿔주면 된다.
state-value bellman equation :
$$ \upsilon _{\pi }(s) = \sum_{a}^{}\pi (a|s)\sum_{s', r}^{}p(s', r|s, a) [r + \gamma\upsilon _{\pi }(s') ] $$
Bellman Optimal State-Value Equation:
$$ \upsilon _{*}(s)=\sum_{a}^{}\pi _{*}(a|s)\sum_{s', r}^{}p(s', r|s, a)[r + \gamma\upsilon _{*}(s') ] $$
$$ \upsilon_{*}(s)=max_{a}(a|s)\sum_{s', r}^{}p(s', r|s, a)[r + \gamma\upsilon_{*}(s')] $$
$ max_{a} $ : $ \sum_{s', r}^{}p(s', r|s, a)[r + \gamma\upsilon_{*}(s')] $ 의 최댓값
$ \upsilon _{*}(s) $를 구하고 그 결과를 이용하면 $ \pi_{*} $도 쉽게 구할 수 있다.
모든 s, a에서 다른 poliicy 보다 우수한 policy를 선택해야 한다.
그러면 우수한 policy를 찾는 방법을 알아보자.
$$ \pi_{*}(s)=argmax_{a}\sum_{s', r}^{}p(s', r|s, a)[r + \gamma\upsilon_{*}(s')] $$
$ argmax_{a} $ : 위 그림에서 S 에서 action을 했을 때 갈 수 있는 next state들에서의 $ p(s', r|s, a)[r + \gamma\upsilon_{*}(s')] $ 중에서 최댓값을 선택
argmax는 리스트 입력값 중에서 가장 큰 숫자의 인덱스를 반환해주는 함수이다.
가장 값이 크다는 것은 최적의 action을 선택한다는 의미이다.
계산을 위해서는 model의 $ p(s', r|s, a) $(전이 확률) 를 알아야 한다.
이 전이 확률을 알 경우 : Model-based
전이 확률을 모를 경우 : Model-free
라고 한다.
대부분의 경우는 Model-free 경우라고 할 수 있다.
Bellman Equation 예제
쉬운 예를 들어서 이 공식이 어떻게 쓰이는지 더 자세히 알아보자.
아래 그림들은 gymnasium에서 재공해주는 환경인 Frozen Lake 에서 가져온 것이다.
https://gymnasium.farama.org/environments/toy_text/frozen_lake/
Gymnasium Documentation
A standard API for reinforcement learning and a diverse set of reference environments (formerly Gym)
gymnasium.farama.org

위 그림을 설명해보자면 마지막 종료 지점인 goal과 fire 지점에서 각각 +1, -1 reward를 얻게 되고, 나머지 state들에서의 reward는 0이다. 물웅덩이에 빠지게 되면 게임이 종료된다.
Deterministic 환경으로 가정하고
$ \gamma =0.9 $ 일때,
$$ \upsilon_{*}(s)=max_{a}(a|s)\sum_{s', r}^{}p(s', r|s, a)[r + \gamma\upsilon_{*}(s')] $$
공식을 이용하여 최적 정책(Optimal Policy)를 발견하여보자.
3차원 공간에서 보고있는 우리는 최적 경로, 즉 optimal policy를 직관적으로 알아볼 수 있다.
하지만 agent는 2차원 공간에 있고, 시행착오를 겪으며 state 하나하나의 value function을 찾아야 한다.
$$ \upsilon_{*}(s)=max_{a}(a|s)\sum_{s', r}^{}p(s', r|s, a)[r + \gamma\upsilon_{*}(s')] $$
에서 Deterministic 환경이라고 가정했기 때문에 $ p(s', r|s, a) = 1 $ 로 간주할 수 있다.
reward r는 맵에서 확인할 수 있고, $ \gamma =0.9 $ 이다.
계산을 해보기 전, MDP 환경에 대해서 다시 한번 짚어보자.
어떠한 state s에 도달했을 때, 이전 state들의 정보를 가지고 있을 필요가 없다. current state에 그 정보가 모두 포함되어 있기 때문이다. 그렇기 때문에 next state s'로 갈 때는 current state s만 고려해야 한다는 내용이었다.
동서남북 action에 대한 reward들을 살펴보도록 하고, goal에서부터 역순으로 계산을 해보자.

goal 옆 state에서의 각 action들의 reward들을 정의하였다. 이때의 argmax()는 right action을 선택하게 될 것이다.
따라서 이 state의 $ \upsilon_{*}(s) = 1 $이 된다.
다음으로 그 위의 state를 구해보면,
right action은 -1이 될 것이고
down action은 $ \gamma\upsilon_{*}(s') $ 에 의해 0.9 * 1 이 될 것이다.
그럼 이 state은 $ \upsilon_{*}(s) = 0.9*1 $이 된다.
값이 정해졌으므로 아래 state에서의 up action의 reward가 새로 갱신되게 된다.

위 과정을 모든 state에서 구해보면 다음과 같이 나오게 된다.

모든 state에서 각 action들의 reward들을 종합하여 각 state에서 최적의 action은 reward가 가장 큰 값을 의미하는 것이다.
따라서 최적의 action들을 맵에 종합하여 보면
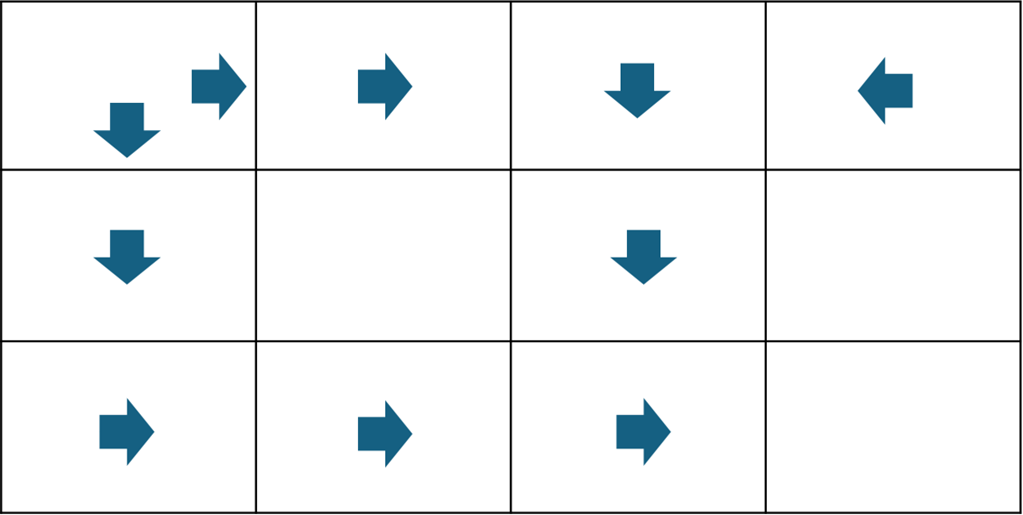
최적 경로를 찾을 수 있게 된다.
'Data Science > 강화학습' 카테고리의 다른 글
| [강화학습] 동적 계획법 - 정책 반복(Policy Iteration) (0) | 2024.10.13 |
|---|---|
| [강화학습] 동적 계획법 - 반복 정책 평가 (Iterative Policy Evaluation) (7) | 2024.10.12 |
| [강화학습] 가치함수(Value Function) (9) | 2024.10.03 |
| [강화학습] 결정론적 vs 확률론적 환경 (Deterministic vs Stochastic Environment) (2) | 2024.10.02 |
| [강화학습] 결정론적 vs 확률론적 정책 (Deterministic vs Stochastic Policy) (1) | 2024.10.02 |